이번에는 부울 대수와 드모르간의 정리에 대해서 알아볼 예정이다.
부울 대수
부울 대수는 AND, OR 그리고 NOT 논리를 이용하여 논리식을 표현한다. 논리식의 각 변수는 0과 1의 값을 가지며, 논리 연산이 가능하다.
부울 대수의 기본 법칙은 아래의 표의 내용과 같다.
| 법칙 | 논리식 |
| 교환법칙 | A + B = B + A |
| 결합법칙 | A + ( B + C ) = ( A + B ) + C |
| 분배법칙 | A ● ( B + C ) = A ● B + A ● C |
부울 정리에 관한 내용은 아래의 표의 내용과 같다.
| 논리 | 논리 연산 | |
| OR 논리 | A + 0 = A | A + 1 = 1 |
| A + A = A | A + A' = 1 | |
| AND 논리 | A ● 0 = 0 | A ● 1 = A |
| A ● A = A | A ● A' = 0 | |
| NOT 논리 | (A')' = A | |
아래의 표는 3 변수(A, B, C) 진리표의 예시이다. 이 진리표를 토대로 부울 정리를 적용해 보고, 회로를 구현해 볼 것이다.
| A | B | C | X |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
위 진리표를 토대로 논리식을 작성해 보면 다음과 같다.
X = A'B'C' + A'B'C + A'BC + AB'C + ABC
위 논리식을 부울 대수와 부울 정리로 간소화하면 다음과 같은 과정을 거치게 된다.
항을 두 개씩 묶어 정리하기 위해 같은 항(A'B'C)을 추가하였다.
X = A'B'(C' + C) + A'C(B' + B) + AC(B' + B)
= A'B' + A'C + AC
= A'B' + C
따라서 위 식은 X = A'B' + C로 정리될 수 있으며, 논리식을 토대로 회로를 구성해 보면 아래와 같이 구현된다.

위 회로를 시뮬레이션하면 아래와 같은 결과가 출력되는 것을 확인할 수 있다.

회로의 시뮬레이션 출력값은 위 진리표와 동일한 것을 확인할 수 있다.
드모르간 정리
드모르간의 정리를 활용하면 AND와 OR의 논리식을 NAND와 NOR의 논리식으로 바꿀 수 있다.
드모르간 제1 정리 : 각 변수를 NOT 한 것의 OR은 NAND와 같다. ( ex : A' + B' = A'B')
드모르간 제2 정리 : 각 변수를 NOT 한 것의 AND는 NOR와 같다. ( ex : A'B' = (A + B)')
이제 드모르간 정리를 활용하여 회로를 구성해 보고 출력해 보자.
드모르간 제1 정리를 바탕으로 구성한 회로는 아래와 같다.

위 회로의 논리식을 도출해 보면 X = A' + B'이고, Y = A'B' 임이 확인된다.
드모르간 제1 정리를 활용해 보면 각 변수를 NOT 한 것의 OR는 NAND와 같으므로, A' + B' = A'B'이 성립되어야 한다.
회로를 시뮬레이션하면 아래와 같은 결과가 출력되는 것을 확인할 수 있다.

X와 Y의 출력 파형은 동일한 것으로 보아, 드모르간 제1 정리는 성립되는 것을 확인할 수 있다.
이번에는 드모르간 제2 정리를 바탕으로 회로를 구성해보려 한다. 회로는 아래와 같다.
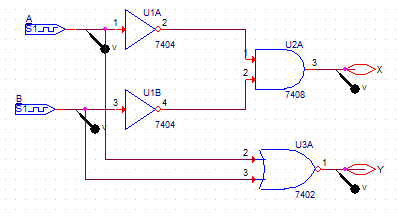
위 회로의 논리식을 도출해 보면 X = A'B', Y = (A + B)' 임이 확인되며, 드모르간 제2 정리에 의해 둘은 같다는 것이 성립되어야 한다.
회로를 시뮬레이션해 보면 다음과 같은 결과가 도출된다.

X와 Y의 출력 파형이 동일한 것으로 보아, 드모르간 제2 정리는 성립된다는 것을 확인할 수 있다.
'Tool > PSpice' 카테고리의 다른 글
| 디지털 회로 실험 : 인코더, 디코더 (0) | 2024.07.08 |
|---|---|
| 디지털 회로 실험 : 멀티플렉서, 디멀티플렉서 (1) | 2024.07.08 |
| 디지털 회로 실험 : 가산기, 감산기 (2) | 2024.06.30 |
| 디지털 회로 실험 : XOR, XNOR 구현 (0) | 2024.06.27 |
| 디지털 회로 실험 : PSpice 회로 시뮬레이션 기초 (0) | 2024.06.26 |